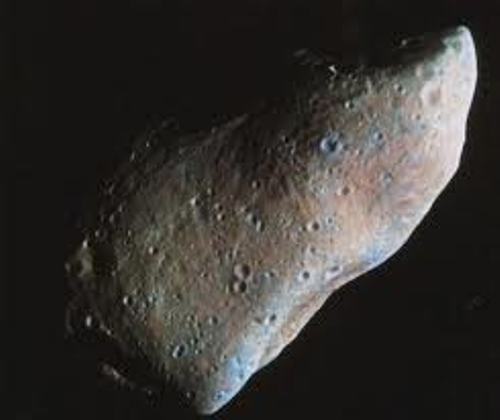
10 Interesting Meteoroid Facts

Kids will love to enjoy Meteoroid Facts.  When you learn about meteoroid, you can find out one of the tiny pieces of space. Meteoroid is always associated with destruction when it comes in big size called asteroid.  Let me show you the interesting facts about meteoroid:

Meteoroid Facts 1: falling of meteoroid

Even though you feel save sleeping at night, you have to know that billions of meteoroids falling to our planet every day. The meteoroid in the size 10 meters fell on earth. It hit just above the Antarctica. It produced 745 tons of dust during the crash.

Meteoroid Facts 2: definition of meteoroid?

Can you define the word meteoroid? Many people still make mistake when defining the meteoroid, meteor and meteorites. Meteoroids are the pieces of debris, dust and rock from the falling comet, asteroid and moons.

Meteoroid Facts

Meteoroid Facts 3: cause of meteoroid creation

Do you know that the collision of asteroid or comet can form the particles or fragment called meteoroid?

Meteoroid Facts 4: size

Let’s talk about the size of Meteoroid. It comes in various sizes from the small one in dirt form into the biggest one in a rock form.

Meteoroid Image

Meteoroid Facts 5: shooting stars

The shooting stars actually are not real stars. They are the burned meteors which collide on the earth atmosphere. They look sparkling on the dark sky.

Meteoroid Facts 6: meteorites

Meteorite is another term used when we talk about meteor and meteoroid. When the chunk of meteoroids falling to the earth does not burn, it will be called meteorite.

Meteoroid on Space

Meteoroid Facts 7: differences of meteor, meteoroid, and meteorites

If you are still confused, let’s find out the difference of meteor, meteorites and meteoroid.  Meteorites are found on the earth ground. Meteors are on the earth atmosphere, while meteoroid is on the space. Check meteor facts here.

Meteoroid Facts 8: craters

Meteoroid can land on moons, asteroids or even planets. If a meteoroid is very big, it can create a powerful crash which leads into the formation of a crater.

Meteoroid Pics

Meteoroid Facts 9: speed

The speed of a meteoroid is very fast. It can travel on earth with the speed at 130,000 miles per hour.

Meteoroid Facts 10: the largest meteorites

Do you know that the largest meteorite was found in 1920 in Namibia, Africa?  It has the dimension of 2.7 m deep, 2.7 m wide and 0.9 m high. The weight of the meteorite is 60 tones. People call it Hoba.

Meteoroid Rock

If the size of a meteoroid is more than 10 meter, you can call it as asteroid. Do you want to shares ideas on facts about meteoroid?